Bono español a 3 años.

• El detalle importante es que la fórmula del precio del bono varía si hay o no abono del cupón corto, el que tiene un importe ligeramente inferior al normal, el cual, como saben, aparece en la denominación del bono.
  • ¿Cuándo se abona el cupón corto? 
    • Cuando la subasta se produce entre la fecha de emisión y el primer abono de cupón.**

** En el caso del bono a 5 años subastado el 17_julio el 31_enero_2025 ya tuvimos un abono de cupón, así que de ahora en adelante las subastas de esta emisión, si llegan a producirse, no tendrán cupón corto, como ha sido el caso en julio y en otras anteriores.

[][][][] Las obligaciones a 10 años subastadas el 17_julio_2025 sí han tenido cupón corto.

Y esto es así porque se emitieron en junio y el cupón se pagará el 31_octubre_2025. Lo podemos ver en el cuadro siguiente. Lo he recortado para que resulte más cómodo.

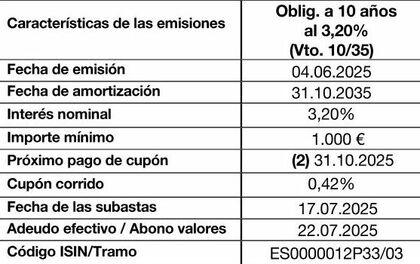
• Fuente Banco de España: https://www.bde.es/f/webbe/INF/MenuHorizontal/entidades-profesionales/operativa_gestiones/comunicaciones/2025/Comu2541.pdf

• 31/10/2025 Interés (primer cupón) 1,306301 y los siguientes cupones regulares, todos iguales.
  1. 31/10/2026 Interés 3,200000
  2. 31/10/2027 Interés 3,200000
  3. 31/10/2028 Interés 3,200000
  4. 31/10/2029 Interés 3,200000
  5. 31/10/2030 Interés 3,200000
  6. 31/10/2031 Interés 3,200000
  7. 31/10/2032 Interés 3,200000
  8. 31/10/2033 Interés 3,200000
  9. 31/10/2034 Interés 3,200000
  10. 31/10/2035 Interés 3,200000
• 31/10/2035 Amortización 100,000000

• Datos:
  • p1 = Días_entre_la_fecha_de_liquidación_y_el_abono_del_primer_cupón / 365.
  • R = 1 + tipo_interés/100
  • Cup = cupón_regular_del_bono #el que se muestra en la denominación del bono u obligación.
  • CC = cupón corto, primer cupón de menor importe, ya que el bono no tiene una duración de n años exactos.
  • Fecha de liquidación / Adeudo / Abono de valores = 22_julio_2025
  • Abono del próximo cupón = 31_octubre_2025
• Sustituimos:
  • p1 = 101/365  
    • #días que faltan para el abono del primer cupón desde el día  22_julio_2027, día de liquidación.
  • R = 1.03303 
    • # 1 + tipo_interés / 100, el tipo medio ha salido al 3,303%
  • CC = 1.306301 
    • # el primer cupón diferente a los demás se calcula desde la fecha de liquidación.
  • Cup = 3.20 
    • #cupón regular.

• Si aplicamos la fórmula para la serie geométrica de la suma de las n primeras potencias de un número, descrita en el post #750, pinchar aquí, tenemos que el Sumatorio se puede acortar.
  • Sumatorio = 1/R * (1 - 1/R**10) / (1 - 1/R)

Python 3.12.3 (main, Jun 18 2025, 17:59:45) [GCC 13.3.0] on linux
Type "help", "copyright", "credits" or "license" for more information.
>>> p1 = 101/365 
>>> R = 1.03303 
>>> CC = 1.306301 
>>> Cup = 3.20 
>>> Sumatorio = 1/R * (1 - 1/R**10) / (1 - 1/R)
>>> Precio_bono = CC / R**p1 + Cup /R**p1 * Sumatorio + 100 /R**(p1 + 10) 
>>> Precio_bono
99.54199272319607

• La web del Tesoro Público nos da el siguiente precio para el Tipo de interés medio, 3,303%.

La diferencia tendría que sacarla con un poco de código, pero no creo que valga la pena, ya he realizado el proceso en numerosas ocasiones y he pegado aquí los posts. No tengo tiempo de más.

La idea de que un aumento sustancial del gasto en defensa desencadenaría una respuesta de los inversores que disciplinaría a los gobiernos no sólo corre el riesgo de alimentar la inacción, sino que es errónea. 

.... la economía rusa tiene aproximadamente el mismo tamaño que la italiana. El PIB de Rusia sólo representa el 10% del de la UE. Además, la población de la UE, unos 450 millones de habitantes, es tres veces mayor que la de Rusia.

Igualar el gasto ruso en defensa -que recientemente se ha elevado al 6% de su PIB- equivaldría a unos 120.000 millones de euros, lo que representa un modesto 0,6% del PIB de la UE. 

.... los gobiernos de toda la UE aumentaron colectivamente el gasto en cuestión de meses a más de 10 veces esa cantidad ante la crisis de Covid. 

Si se gasta más en defensa con un presupuesto fijo, ..., algo más tendrá que ceder. Para algunos comentaristas, esto significa recortes políticamente difíciles en el gasto social.

China, Japón, EE.UU. y el Reino Unido tienen ratios de deuda en relación con el PIB más elevados -de hecho, mucho, mucho más elevados- que la UE.

... la UE podría emitir más deuda colectiva para contribuir a financiar el aumento de la defensa.

Al mismo tiempo, una mayor emisión colectiva aumentaría la reserva de capital para impulsar el crecimiento económico interno. 

El propio gasto en defensa aumentaría el crecimiento, aun aceptando que probablemente sea menor que el de otros tipos de gasto público. 

Y una vuelta a la media de crecimiento anual de la UE anterior a la pandemia, del 1,4% en términos reales, compensaría con creces el aumento necesario para garantizar la seguridad de Europa.

El FMI ha calculado que la reducción de las barreras internas de la UE al comercio podría impulsar la productividad en la friolera de siete puntos porcentuales ...

Los puntos aquí expuestos ponen de relieve que las barreras en Europa no son económicas, sino políticas.

Pero la actual situación de soberanía es una ilusión.

Los Estados miembros, como ilustra de forma quizá más destacada Alemania, dependen actualmente de países de fuera de Europa para el crecimiento, la energía y la seguridad.

.... las barreras en Europa no son económicas, sino políticas.

Lo dicen en voz baja, pero los bancos centrales han desempeñado un importante papel de apoyo durante esta era de laxitud fiscal. Sus compras directas de deuda pública -la relajación cuantitativa- alcanzaron un máximo de más de 10 billones de dólares, alrededor de un tercio del saldo vivo en ese momento.

La fase posterior de la QE, incluidas las compras realizadas en respuesta a Covid-19, es más difícil de justificar. Con una política fiscal altamente expansiva, el principal objetivo de la QE era aplacar a los inquietos mercados de bonos en lugar de impulsar la inflación. 

Reconociendo esto, mi impresión es que en el futuro los bancos centrales recurrirán más a los acuerdos de recompra a largo plazo (repos), en lugar de a la QE, para aliviar las tensiones del mercado de bonos. En un mundo de tipos de interés reales más altos, es posible que la QE ya no sea tan necesaria con fines cíclicos.

Pero la QE es sólo un camino hacia el dominio fiscal. El otro es la presión sobre los bancos centrales para que bajen los tipos de interés con el fin de frenar los costes del servicio de la deuda. 

En sus recientes críticas a la Reserva Federal, Trump hizo una estimación precisa de la magnitud y el origen de los beneficios de unos tipos más bajos: 360.000 millones de dólares al año en reducción de los costes de refinanciación del Gobierno por punto porcentual. Esto indica una forma mucho más fuerte de dominio fiscal por la puerta delantera.

Dado que los bancos centrales afectan principalmente a los tipos de interés a corto plazo, el riesgo es más grave cuando los vencimientos de la deuda pública son cortos y se acortan. En Estados Unidos, dos tercios de la deuda pública en circulación tienen ahora un vencimiento inferior a cinco años. El año pasado, alrededor de un tercio de la deuda emitida tenía un vencimiento inferior a un año. Esta tendencia se refleja a escala internacional.

La deuda pública del Reino Unido tiene un vencimiento medio ponderado de más de 14 años. Pero este plazo también ha ido disminuyendo, y la emisión de deuda prevista tiene un vencimiento medio de nueve años. La tendencia a la emisión a corto plazo también se ha observado en Canadá, Alemania, Francia y otros países de la OCDE. Más del 40% de los más de 50 billones de dólares de deuda soberana de la OCDE tendrán que refinanciarse en los próximos tres años.

Ante el pronunciamiento de las curvas de rendimiento, estas estrategias de endeudamiento tienen sentido desde el punto de vista fiscal. Sin embargo, sus consecuencias monetarias pueden no ser tan benignas...

 .....los mercados emergentes tienden a tener vencimientos de deuda más cortos y una independencia de los bancos centrales más débil.

 Si la mayor economía y el banco central más poderoso del mundo no es inmune al populismo fiscal, tampoco lo es nadie.

Me despido hasta otra ocasión con un enlace al pdf del comentario semanal de BlackRock.

• https://www.blackrock.com/corporate/literature/market-commentary/weekly-investment-commentary-en-us-20250721-a-new-regime-for-income-in-portfolios.pdf

No tengo tiempo de pegar la traducción. Si no son amigos de los idiomas pueden recurrir a DeepL. El texto está en inglés. Sobre los bonos gubernamentales europeos dice lo siguiente.

We are neutral. Yields are attractive, and term premium has risen closer to our expectations relative to U.S. Treasuries. We prefer peripheral bonds such as in Italy and Spain.