Pensando tranquilamente el otro día mientras leía bajo la luz de mi lampara de escritorio con los tickers de bolsa moviéndose de un lado a otro en mi ordenador, se me ocurrió que una de las entradas que debía hacer era la de comunicar, de alguna manera, una forma de "mejorar" o "maximizar" la forma en la que podía transmitir la importancia del control de riesgos a la hora de crear una cartera de valores. Y evidentemente no se me podría haber ocurrido otra cosa que explicar de manera sencilla algo que ya muchos (supongo) sabréis, que es la diferencia existente que hay entre el riesgo sistemático y el no sistemático, así como la manera más inteligente de abordar el no sistemático, que a fin de cuentas es lo único que "controlamos". Procederé a mostrar un post lo más corto posible para no aburrir al personal, pero intentando ser lo más preciso posible, vayamos a ello.
TIPOS DE RIESGO BÁSICOS
La palabra "riesgo" es una palabra ciertamente engañosa. El riesgo puede ser muy diferentes según el tipo de inversor que seas, para un inversor cuantitativo el riesgo puede tener mucho que ver con la volatilidad del activo (y no solo cuantitativo, sino a nivel institucional también), sin embargo para un inversor Value el riesgo puede cobrar un tinte muy diferente. Desde mi punto de vista, considero que es bastante importante, sin embargo, entender que el riesgo tiene dos subdivisiones:
Riesgo Total = Riesgo sistemático + Riesgo NO sistemático
Tanto el sistemático como el no sistemático son dos riesgos diferentes que afectan de la misma manera a la cotización de un activo. Solo uno de ellos es inevitable.
- RIESGO SISTEMÁTICO: Al riesgo sistemático se le conoce como "riesgo de mercado" y está presente en todos los activos. Es el llamado riesgo inevitable y tiene mucho que ver con las expectativas de rentabilidad de los inversores sobre dicho activo.
- RIESGO NO SISTEMÁTICO: El riesgo no sistemático, por su lado, engloba todos aquellos factores propios de una empresa, digamos que su base es la incertidumbre de mercado y tienen mucho que ver con las "tripas" de dichas empresas. Por ejemplo, un riesgo no sistemático es que una empresa pierda un litigio, o que los resultados empresariales bajen año tras año, que se detecte fraude en sus cuentas etc. Este riesgo, al contrario que el anterior, SI es inevitable, veremos cómo.
EL PODER DE LA DIVERSIFICACIÓN
Aún recuerdo cuando leí hace mucho tiempo a Warren Buffet exponiendo algo así a que "si se tiene un buen conocimiento sobre lo que se está haciendo, diversificar es un error", menudo mito cayó aquel día...
La diversificación en cartera ha sido demostrada necesaria de manera sistemática año tras año, estudio tras estudio. Es de las pocas cosas/verdades a nivel financiero que ha sido capaz de mantenerse vigente a lo largo del tiempo y ha conseguido no solo mejorar los rendimientos en contra de las carteras menos diversificadas (hasta cierto nivel), sino evitar que muchos fondos colapsaran demasiado rápido. De hecho el CAPM tuvo sus inicios a raíz de la tesis que pretende solucionar la cultura de la diversificación: reducir el riesgo no sistemático.
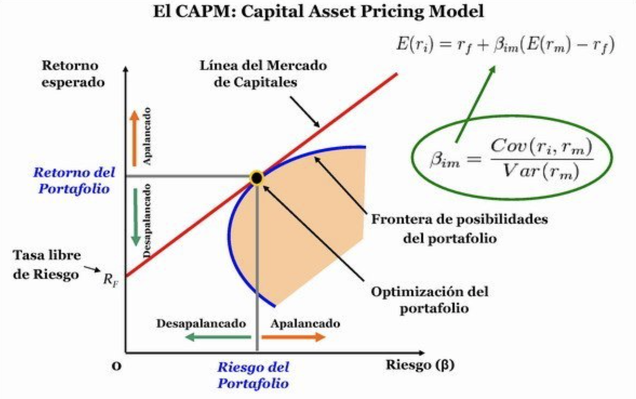
Y sí amigos, si nos fijamos en el modelo (el cual ya comenté en el post anterior que no es muy fiable que digamos porque parte de unas premisas equivocadas), aunque imperfecto, descubrimos que guarda una parte muy interesante en su formula. A saber que, la primera parte de la misma se refiere a la parte sistemática (rf) mientras que la segunda a la no sistemática (Bm(E(Rm)-rf)), y es esta, la segunda parte, la que no demuestra que la diversificación es capaz de reducir considerablemente el riesgo global, puesto que esta nos indica que necesita una Beta concreta. Esta beta, si la operamos según la teoría moderna de carteras (Markowitz) nos indica que a mas acciones tengamos en cartera, la beta de la misma cambiará según la interpelación no solo de las acciones con su mercado principal, sino entre ellas mismas. Y eh aquí la clave:
A la hora de reducir la beta de mercado, NO solo debemos elegir activos (de entre varios candidatos) con betas menores, sino que entre ellos, la sensibilidad correlativa sea lo menor posible.
En castellano: Si quieres tener una buena cartera de inversión, una vez tengas candidatos, no solo debes buscar acciones que tengan baja sensibilidad (Beta) con respecto a su activo de referencia, sino que también deben estar descorrelacionadas entre ellas, que seanindependientes linealmente entre ellas.
CORRELACION Y CRITERIO DE INDEPENDENCIA LINEAL, CÓDIGO DE EJEMPLO
Obviamente no estoy descubriendo nada nuevo aquí, pero me gusta a veces recordar este tipo de premisas básicas a la hora de formar una cartera de inversión, puesto que a veces nos surge la duda de la descorrelación que pueda haber entre dos empresas. Además, muchas páginas por internet muestran las betas como si de algo mágico fuera, y lo cierto es que ese dato y nada es lo mismo, puesto que la beta suele variar mucho. Por ejemplo, un histórico de la evolución de la beta de Red eléctrica los últimos 10 años:
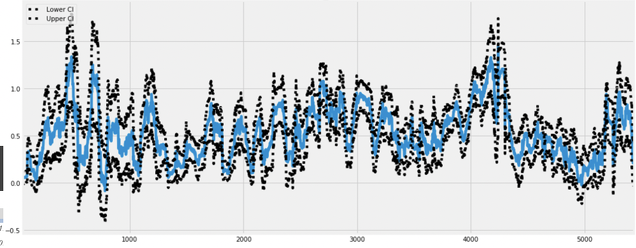
Entonces, ¿Qué nos queda?. Nos queda buscar las empresas lo más descorrelacinadas entre sí posible, por eso, y como decía en el párrafo anterior, es importante tener un abanico grande de candidatos a inversión. Por ejemplo, si queremos tener una cartera de 10 activos, y tenemos 15 candidatos, debemos coger de entre esos 15, los más descorrelacionados entre ellos, es decir, "más independientes linealmente hablando entre ellos a lo largo de una serie de valores (no en el momento actual)". Esto se suele hacer con matriz de varianzas covarianzas filtradas durante varios años o con otros métodos más específicos. Personalmente suelo usar paquetes en R o en Python para esta función, facilitan bastante la labor y hace que uno tome decisiones más rápido (al final del post os pongo el código de independencia lineal en el que de entre un conjunto de activos candidatos, este calcula los "x" valores (subtamaño) de dicho conjunto más independientes entre ellos, pero ojo que falta la carga de paquetes y de valores, tan solo os pongo el código de lo que hablamos en este post, puesto que tampoco esto es un blog de análisis cuantitativo, si alguien quiere el código íntegro que me lo comunique por privado), sin embargo mi máxima a la hora de aconsejar a amigos y gente que me pregunta y que no tiene conocimientos de programación o que no quieren complicarse la vida, suele ser la misma: Intenta maximizar la diversidad de sectores, países y tipos de empresas, a más diversificado entre aspectos empresariales (sector, país, materia prima etc), más probabilidades habrá de que exista una independencia lineal entre dichas empresas y, por consiguiente, más reducirás tu riesgo no sistemático.
Un saludo, y nos vemos en el próximo post!
CÓDIGO INDEPENDENCIA INTERCORRELATIVA:



